C# 傅里叶变换
AForge.NET/ComplexImage.cs at master · andrewkirillov/AForge.NET
AForge.NET/FourierTransform.cs at master · andrewkirillov/AForge.NET
抽空去试试这个源码
是C语言实现的
感觉不错,抽空去试试
别人给出了数据计算后的例子
目的: 做傅里叶变换, 得到T在各个频率上的振幅
原先数据:
new_Signal = x^2 + y^2 =[0.077641, 0.070009, 0.086816, 0.180072, 0.218088, 0.110777,0.067657, 0.108425, 0.13954 , 0.13954 , 0.195336, 0.165397,0.146461, 0.107648, 0.056641, 0.135629] |
傅里叶变换后是:
FreqAmp = [ 2.005677 +0.j , -0.1811103 +0.01788887j, -0.22535551-0.22328895j, -0.00423924+0.23675752j, 0.17528 +0.161549j , 0.04949067-0.04438796j, -0.06938049+0.09241905j, -0.11173713+0.02325139j, -0.029317 +0.j , -0.11173713-0.02325139j, -0.06938049-0.09241905j, 0.04949067+0.04438796j, 0.17528 -0.161549j , -0.00423924-0.23675752j, -0.22535551+0.22328895j, -0.1811103 -0.01788887j] |
现在要去想办法去用C#实现上述的计算结果
c# fourier transform code
可以考虑是试试这个:
具体实现:
AForge.NET/FourierTransform.cs at master · andrewkirillov/AForge.NET · GitHub
使用范例:
AForge.NET/ComplexImage.cs at master · andrewkirillov/AForge.NET · GitHub
不过有微软官网的
去看看
直接贴出源码了
要去搞清楚如何使用
也有直接的代码
结果用:
using System; using System.Numerics; using System; using System.Numerics; namespace FUYI_Client { class crifanFFT { // Fast Fourier Transform in C# /* Performs a Bit Reversal Algorithm on a postive integer * for given number of bits * e.g. 011 with 3 bits is reversed to 110 */ public static int BitReverse(int n, int bits) { int reversedN = n; int count = bits – 1; n >>= 1; while (n > 0) { reversedN = (reversedN << 1) | (n & 1); count–; n >>= 1; } return ((reversedN << count) & ((1 << bits) – 1)); } /* Uses Cooley-Tukey iterative in-place algorithm with radix-2 DIT case * assumes no of points provided are a power of 2 */ public static void FFT(Complex[] buffer) { int bits = (int)Math.Log(buffer.Length, 2); for (int j = 1; j < buffer.Length / 2; j++) { int swapPos = BitReverse(j, bits); var temp = buffer[j]; buffer[j] = buffer[swapPos]; buffer[swapPos] = temp; } for (int N = 2; N <= buffer.Length; N <<= 1) { for (int i = 0; i < buffer.Length; i += N) { for (int k = 0; k < N / 2; k++) { int evenIndex = i + k; int oddIndex = i + k + (N / 2); var even = buffer[evenIndex]; var odd = buffer[oddIndex]; double term = -2 * Math.PI * k / (double)N; Complex exp = new Complex(Math.Cos(term), Math.Sin(term)) * odd; buffer[evenIndex] = even + exp; buffer[oddIndex] = even – exp; } } } } } } private void testFftToolStripMenuItem_Click(object sender, EventArgs e) { Log(“test FFT”); //Complex[] input = { 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0 }; Complex[] input = { 0.077641, 0.070009, 0.086816, 0.180072, 0.218088, 0.110777, 0.067657, 0.108425, 0.13954, 0.13954, 0.195336, 0.165397, 0.146461, 0.107648, 0.056641, 0.135629 }; crifanFFT.FFT(input); Console.WriteLine(“Results:”); foreach (Complex c in input) { Console.WriteLine(c); } } |
测试结果,除了第一个和预期一致,其他都不一样
(2.005677, 0) (-0.0440878098072094, 0.0563375488458987) (-0.0940835140038455, -0.272891535410738) (-0.203768798154086, 0.0126622006202) (-0.087264, 0.046051) (0.0633735877860757, 0.179707364194415) (0.0618915140038455, 0.305360464589262) (-0.0631129798247799, -0.0151972875798867) (-0.0293169999999998, 0) (-0.0631129798247799, 0.0151972875798867) (0.0618915140038455, -0.305360464589262) (0.0633735877860758, -0.179707364194415) (-0.087264, -0.046051) (-0.203768798154086, -0.0126622006202) (-0.0940835140038455, 0.272891535410738) (-0.0440878098072094, -0.0563375488458987) |
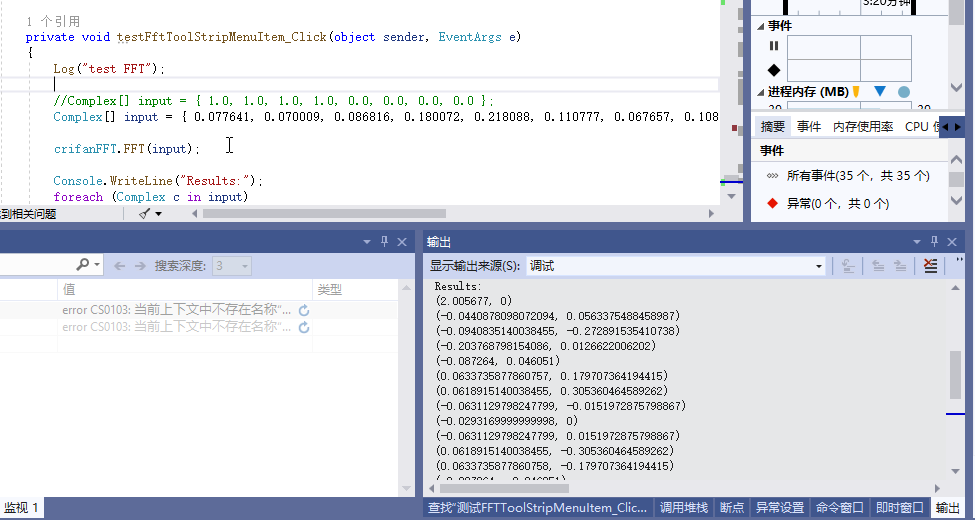
所以只能再去换别的写法
然后换成:
/// <summary>
/// Provides the Discrete Fourier Transform for a real-valued input signal
/// </summary>
/// <param name="input">the signal to transform</param>
/// <param name="partials">the maximum number of partials to calculate. If not value is given it defaults to input/2</param>
/// <returns>The Cos and Sin components of the signal, respectively</returns>
public static Tuple<double[], double[]> DFT(double[] input, int partials = 0)
{
int len = input.Length;
double[] cosDFT = new double[len / 2 + 1];
double[] sinDFT = new double[len / 2 + 1];
if (partials == 0)
partials = len / 2;
for (int n = 0; n <= partials; n++)
{
double cos = 0.0;
double sin = 0.0;
for (int i = 0; i < len; i++)
{
cos += input[i] * Math.Cos(2 * Math.PI * n / len * i);
sin += input[i] * Math.Sin(2 * Math.PI * n / len * i);
}
cosDFT[n] = cos;
sinDFT[n] = sin;
}
return new Tuple<double[], double[]>(cosDFT, sinDFT);
}
double[] input = { 0.077641, 0.070009, 0.086816, 0.180072, 0.218088, 0.110777, 0.067657, 0.108425, 0.13954, 0.13954, 0.195336, 0.165397, 0.146461, 0.107648, 0.056641, 0.135629 };
Tuple<double[], double[]> output = crifanDFT.DFT(input);
double[] outputList1 = output.Item1;
double[] outputList2 = output.Item2;
Console.WriteLine("Results:");
int curIdx = 0;
foreach (double curItem1Value in outputList1)
{
Console.WriteLine("[{0}]={{{1}, {2}}}", curIdx, curItem1Value, outputList2[curIdx]);
curIdx++;
}结果竟然是:
计算的结果:
[0]={2.005677, 0}
[1]={-0.181110302258433, -0.0178888702258191}
[2]={-0.225355514003845, 0.223288954424222}
[3]={-0.00423923852817759, -0.236757522000121}
[4]={0.175279999999999, -0.161549}
[5]={0.0494906709200072, 0.0443879571855055}
[6]={-0.0693804859961551, -0.092419045575778}
[7]={-0.111737130133397, -0.0232513910401929}
[8]={-0.029317, 8.53570355076414E-16}是和预期的,基本一致,除了最后一个
但是16个输入的值
输出的tuple,用于表示复数,竟然只有10个了:
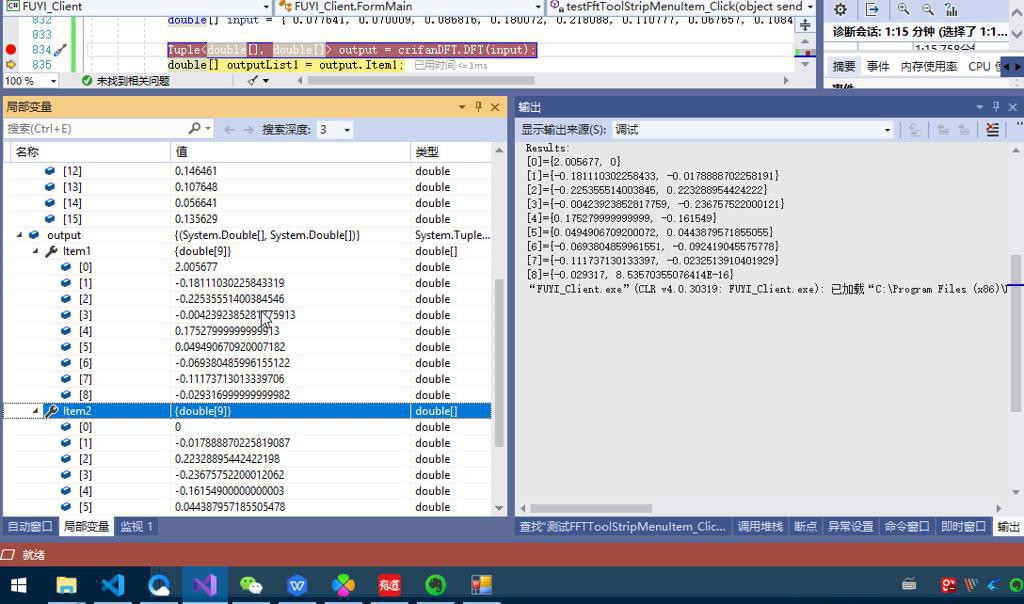
很是奇怪,所以要去找找原因
去调试,才看清,原来默认只计算length/2的个数
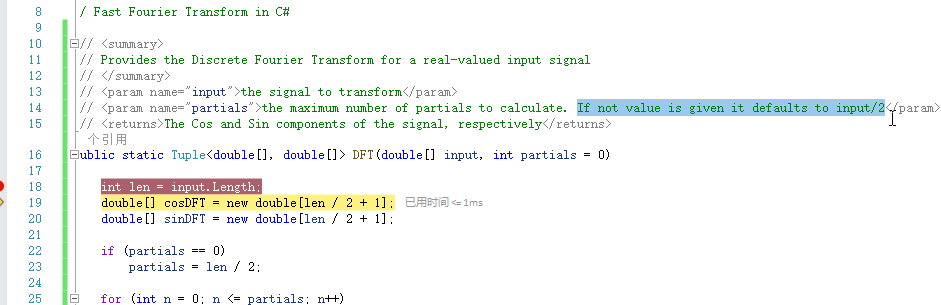
所以传入原始数组长度,再去计算看看结果是否完全符合预期
Tuple<double[], double[]> output = crifanDFT.DFT(input, partials:input.Length);
结果:
内部报错
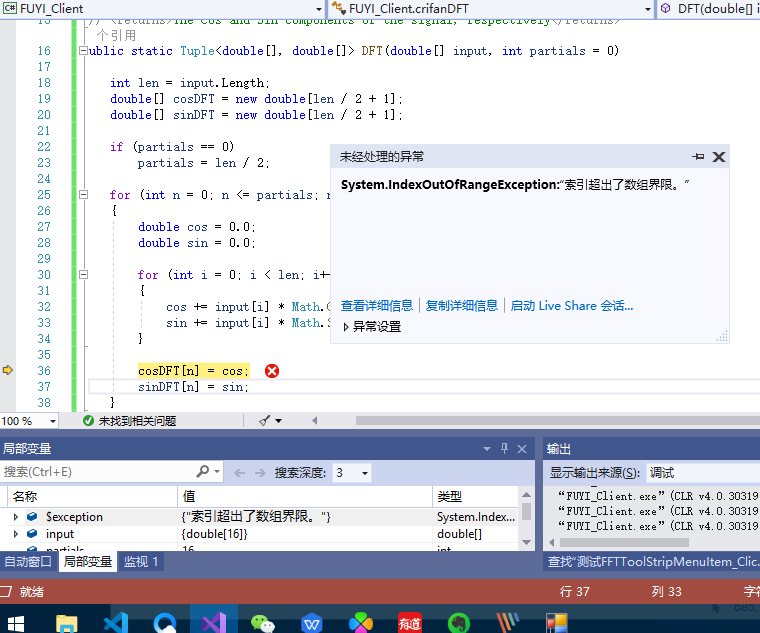
原来是cos和sin的数组长度也不对,没有变回来传入的长度
所以去改为:
/// <summary>
/// Provides the Discrete Fourier Transform for a real-valued input signal
/// </summary>
/// <param name="input">the signal to transform</param>
/// <param name="partials">the maximum number of partials to calculate. If not value is given it defaults to input/2</param>
/// <returns>The Cos and Sin components of the signal, respectively</returns>
public static Tuple<double[], double[]> DFT(double[] input, int partials = 0)
{
int len = input.Length;
if (partials == 0)
partials = len / 2;
//double[] cosDFT = new double[len / 2 + 1];
//double[] sinDFT = new double[len / 2 + 1];
double[] cosDFT = new double[partials];
double[] sinDFT = new double[partials];
//if (partials == 0)
// partials = len / 2;
//for (int n = 0; n <= partials; n++)
for (int n = 0; n < partials; n++)
{
double cos = 0.0;
double sin = 0.0;
for (int i = 0; i < len; i++)
{
cos += input[i] * Math.Cos(2 * Math.PI * n / len * i);
sin += input[i] * Math.Sin(2 * Math.PI * n / len * i);
}
cosDFT[n] = cos;
sinDFT[n] = sin;
}
return new Tuple<double[], double[]>(cosDFT, sinDFT);
}结果:
是可以输出我们希望的结果的
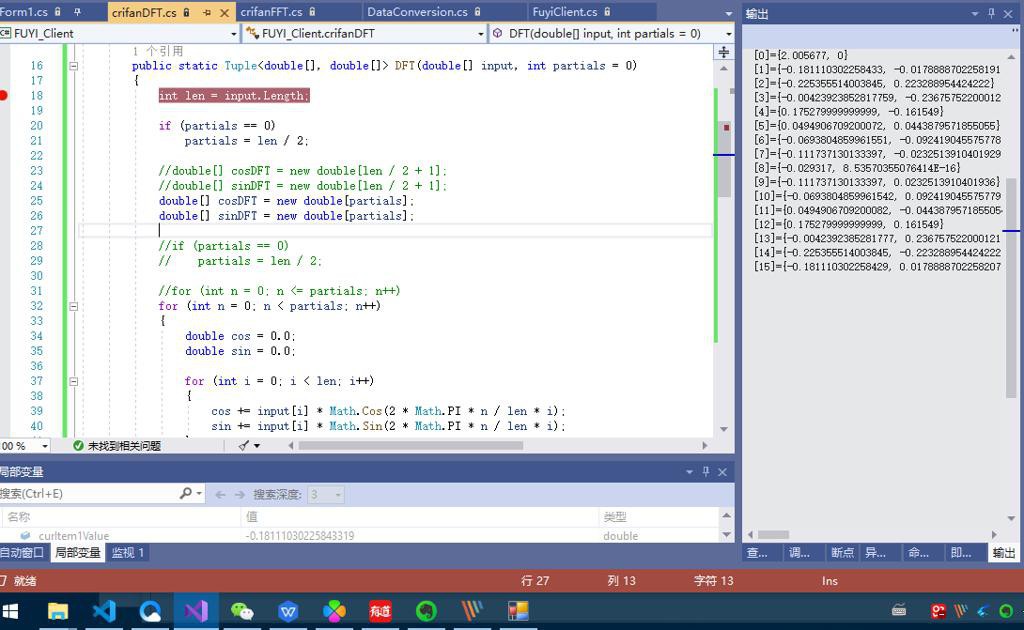
输入:
double[] input = { 0.077641, 0.070009, 0.086816, 0.180072, 0.218088, 0.110777, 0.067657, 0.108425, 0.13954, 0.13954, 0.195336, 0.165397, 0.146461, 0.107648, 0.056641, 0.135629 };输出:
[0]={2.005677, 0}
[1]={-0.181110302258433, -0.0178888702258191}
[2]={-0.225355514003845, 0.223288954424222}
[3]={-0.00423923852817759, -0.236757522000121}
[4]={0.175279999999999, -0.161549}
[5]={0.0494906709200072, 0.0443879571855055}
[6]={-0.0693804859961551, -0.092419045575778}
[7]={-0.111737130133397, -0.0232513910401929}
[8]={-0.029317, 8.53570355076414E-16}
[9]={-0.111737130133397, 0.0232513910401936}
[10]={-0.0693804859961542, 0.092419045575779}
[11]={0.0494906709200082, -0.0443879571855054}
[12]={0.175279999999999, 0.161549}
[13]={-0.0042392385281777, 0.236757522000121}
[14]={-0.225355514003845, -0.223288954424222}
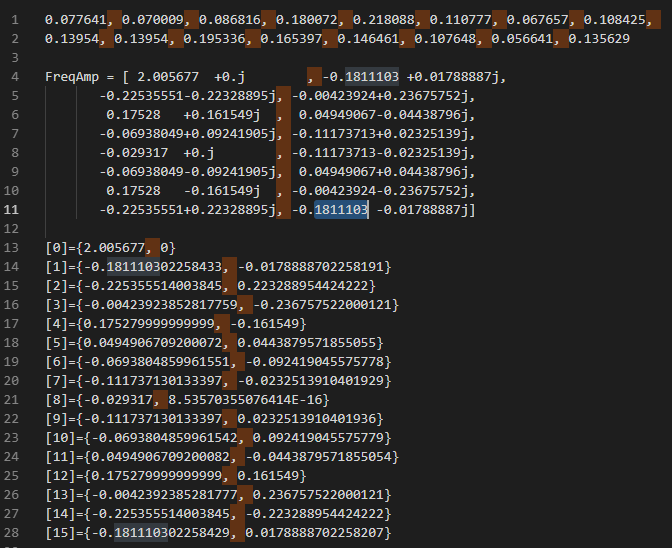
[15]={-0.181110302258429, 0.0178888702258207}对比后发现是我们要的
【总结】
目前,对于数据:
输入:
[0.077641, 0.070009, 0.086816, 0.180072, 0.218088, 0.110777,0.067657, 0.108425, 0.13954 , 0.13954 , 0.195336, 0.165397,0.146461, 0.107648, 0.056641, 0.135629]
可以通过C#代码:
crifanDFT.cs
using System;
using System.Numerics;
namespace FUYI_Client
{
class crifanDFT
{
// Fast Fourier Transform in C#
/// <summary>
/// Provides the Discrete Fourier Transform for a real-valued input signal
/// </summary>
/// <param name="input">the signal to transform</param>
/// <param name="partials">the maximum number of partials to calculate. If not value is given it defaults to input/2</param>
/// <returns>The Cos and Sin components of the signal, respectively</returns>
public static Tuple<double[], double[]> DFT(double[] input, int partials = 0)
{
int len = input.Length;
if (partials == 0)
partials = len / 2;
//double[] cosDFT = new double[len / 2 + 1];
//double[] sinDFT = new double[len / 2 + 1];
double[] cosDFT = new double[partials];
double[] sinDFT = new double[partials];
//if (partials == 0)
// partials = len / 2;
//for (int n = 0; n <= partials; n++)
for (int n = 0; n < partials; n++)
{
double cos = 0.0;
double sin = 0.0;
for (int i = 0; i < len; i++)
{
cos += input[i] * Math.Cos(2 * Math.PI * n / len * i);
sin += input[i] * Math.Sin(2 * Math.PI * n / len * i);
}
cosDFT[n] = cos;
sinDFT[n] = sin;
}
return new Tuple<double[], double[]>(cosDFT, sinDFT);
}
/// <summary>
/// Takes the real-valued Cos and Sin components of Fourier transformed signal and reconstructs the time-domain signal
/// </summary>
/// <param name="cos">Array of cos components, containing frequency components from 0 to pi. sin.Length must match cos.Length</param>
/// <param name="sin">Array of sin components, containing frequency components from 0 to pi. sin.Length must match cos.Length</param>
/// <param name="len">
/// The length of the output signal.
/// If len < (partials-1)*2 then frequency data will be lost in the output signal.
/// if no len parameter is given it defaults to (partials-1)*2
/// </param>
/// <returns>the real-valued time-domain signal</returns>
public static double[] IDFT(double[] cos, double[] sin, int len = 0)
{
if (cos.Length != sin.Length) throw new ArgumentException("cos.Length and sin.Length bust match!");
if (len == 0)
len = (cos.Length - 1) * 2;
double[] output = new double[len];
int partials = sin.Length;
if (partials > len / 2)
partials = len / 2;
for (int n = 0; n <= partials; n++)
{
for (int i = 0; i < len; i++)
{
output[i] += Math.Cos(2 * Math.PI * n / len * i) * cos[n];
output[i] += Math.Sin(2 * Math.PI * n / len * i) * sin[n];
}
}
return output;
}
}
}注:此处暂时没用到IDFT,以备后用
测试代码:
double[] input = { 0.077641, 0.070009, 0.086816, 0.180072, 0.218088, 0.110777, 0.067657, 0.108425, 0.13954, 0.13954, 0.195336, 0.165397, 0.146461, 0.107648, 0.056641, 0.135629 };
//Tuple<double[], double[]> output = crifanDFT.DFT(input);
Tuple<double[], double[]> output = crifanDFT.DFT(input, partials:input.Length);
double[] outputList1 = output.Item1;
double[] outputList2 = output.Item2;
Console.WriteLine("Results:");
int curIdx = 0;
foreach (double curItem1Value in outputList1)
{
Console.WriteLine("[{0}]={{{1}, {2}}}", curIdx, curItem1Value, outputList2[curIdx]);
curIdx++;
}
}可以输出我们要的结果:
Results:
[0]={2.005677, 0}
[1]={-0.181110302258433, -0.0178888702258191}
[2]={-0.225355514003845, 0.223288954424222}
[3]={-0.00423923852817759, -0.236757522000121}
[4]={0.175279999999999, -0.161549}
[5]={0.0494906709200072, 0.0443879571855055}
[6]={-0.0693804859961551, -0.092419045575778}
[7]={-0.111737130133397, -0.0232513910401929}
[8]={-0.029317, 8.53570355076414E-16}
[9]={-0.111737130133397, 0.0232513910401936}
[10]={-0.0693804859961542, 0.092419045575779}
[11]={0.0494906709200082, -0.0443879571855054}
[12]={0.175279999999999, 0.161549}
[13]={-0.0042392385281777, 0.236757522000121}
[14]={-0.225355514003845, -0.223288954424222}
[15]={-0.181110302258429, 0.0178888702258207}转载请注明:在路上 » 【已解决】C# 傅里叶变换